排序算法
插入排序 insertion sort
插入排序应该算是最简单和容易理解的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应�位置并插入。具有 n 个元素时它需要经过 n-1 趟排序。对于 p = 1 到 p = n-1 趟,插入排序保证从位置 0 到位置 p 上的元素为已排序状态。它就是基于这个事实来排序的。
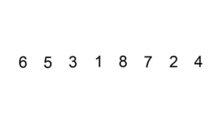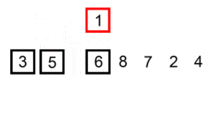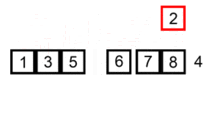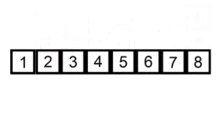
function sort(arr) {
if(arr.length <= 1) {
return arr
}
for(var i=0; i<arr.length; i++) {
for(var j=i-1; j>=0; j--) {
if(arr[j+1] < arr[j]) {
var temp = arr[j+1];
arr[j+1] = arr[j];
arr[j] = temp
}
}
}
return arr
}
如果目标是把 n 个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有 n(n-1)/2 次。插入排序的赋值操作是比较操作的次数减去(n-1)次。平均来说插入排序算法复杂度为 O(n^2)。因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。 插入排序在工业级库中也有着广泛的应用,在 STL 的 sort 算法和 stdlib 的 qsort 算法中,都将插入排序作为快速排序的补充,用于少量元素的排序(通常为 8 个或以下)
冒泡排序 bubble sort
冒泡排序是与插入排序拥有相等的运行时间,但是两种算法在需要的交换次数却很大地不同。在最好的情�况,冒泡排序需要 O(n^2)次交换,而插入排序只要最多 O(n)交换。冒泡排序的实现(类似下面)通常会对已经排序好的数列拙劣地运行 O(n^2),而插入排序在这个例子只需要 O(n)个运算。因此很多现代的算法教科书避免使用冒泡排序,而用插入排序替换之。冒泡排序如果能在内部循环第一次运行时,使用一个旗标来表示有无需要交换的可能,也可以把最好的复杂度降低到 O(n)。在这个情况,已经排序好的数列就无交换的需要。若在每次走访数列时,把走访顺序反过来,也可以稍微地改进效率。有时候称为鸡尾酒排序,因为算法会从数列的一端到另一端之间穿梭往返。
冒泡排序算法的运作如下:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
由于它的简洁,冒泡排序通常被用来对于程序设计入门的学生介绍算法的概念。
function bubbleSort(arr) {
if(arr.length <= 1) {
return arr;
}
for(var j=0; j<arr.length; j++) {
for(var i=0; i<arr.length-j; i++) {
if(arr[i] > arr[i+1]) {
var tmp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = tmp;
}
}
}
return arr;
}
选择排序(selection sort)
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对 n 个元素的表进行排序总共进行至多 n-1 次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
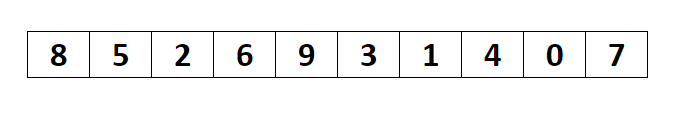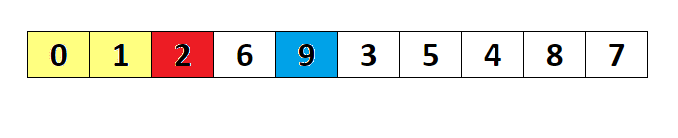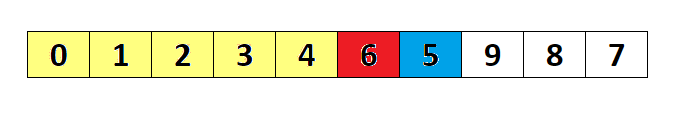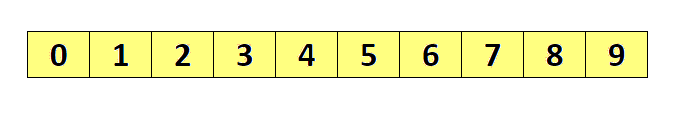
复杂度分析
选择排序的交换操作介于 0 和(n-1)次之间。选择排序的比较操作为 n(n-1)/2 次之间。选择排序的赋值操作介于 0 和 3(n-1)次之间。比较次数 O(n^2),比较次数与关键字的初始状态无关,总的比较次数 N=(n-1)+(n-2)+...+1=n(n-1)/2。交换次数 O(n),最好情况是,已经有序,交换 0 次;最坏情况是,逆序,交换 n-1 次。交换次数比冒泡排序较少,由于交换所需 CPU 时间比比较所需的 CPU 时间多, n 值较小时,选择排序比冒泡排序快。
原地操作几乎是选择排序的唯一优点,当空间复杂度要求较高时,可以考虑选择排序;实际适用的场合非常罕见。
function selectionSort(arr) {
if(arr.length <= 1) {
return arr
}
var i, j, min;
var temp;
for (i = 0; i < arr.length - 1; i++) {
min = i;
for (j = i + 1; j < arr.length; j++) {
if (arr[min] > arr[j])
min = j;
temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
return arr
}
快速排序(quick sort)
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
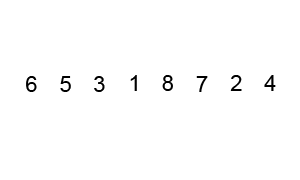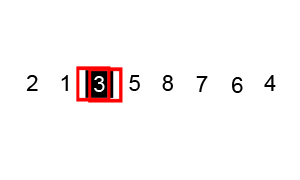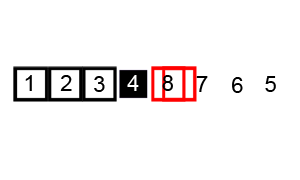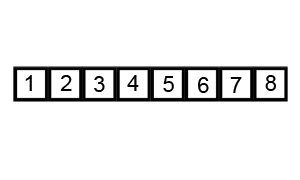
步骤为:
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
正如它的名字,快速排序是在时间中最快的已知排序算法,它的平均运行时间是 O(NlogN)。快速排序也是一种分治的递归算法。将数组 S 排序的基本算法由下列简单的四步组成:
- 如果 S 中元素个数是 0 或 1,则返回
- 取 S 中任一元素 v,称之为枢纽元
- 将 S - {v}分成两个不相交的集合:S1 = {x∈S - {v} | x ≤ v}和 S2 = {x∈S - {v} | x ≥ v}
- 返回{quicksort(S1)},继续 v,继而 quicksort(S2)
由于对枢纽元的处理会导致第三步中的分割不唯一,因此,我们希望把等于枢纽元的大约一半的关键字分到 S1 中,而另外一半分到 S2 中,那怎么去选择一个好的枢纽元呢?
选取枢纽元
一种错误的方法
通常的,没有经过充分考虑的选择是将第一个元素用作枢纽元。如果输入是随机的,那么这是可以接受的,但是如果输入是预排序或是反序的,那么这样的枢纽元就会产生一个劣质的分割,因为所有的元素不是都被划入 S1 就是被划入 S2。
一种安全的作法
一种安全的方针是随机选取枢纽元。但是另一方面,随机数的生成一般是昂贵的,根本减少不了算法奇遇部分的平均运行时间。
三数中值分割法
一组 N 个数的中值是第 Math.ceil(N/2)个最大的数。枢纽元的最好的选择是数组的中值。不幸的是,这很难算出,且会减慢快速排序的速度。因此一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元。例如,输入为 8, 1, 4, 9, 6, 3, 5, 2, 7, 0,它的左边元素是 8,右边元素是 0,中心位置为 Math.floor((left + right) / 2)上的元素是 6,于是枢纽元 v=6。
function quickSort(arr) {
if (arr.length <= 1) {
return arr.slice(0);
}
var left = [];
var right = [];
var mid = [arr[0]]; //first number as a pivot
for (var i = 1; i < arr.length; i++) {
if (arr[i] < mid[0]) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat(mid.concat(quickSort(right)));
}