默克尔树
默克尔树是区块链技术的一个基本概念。它们是一种特殊的二进制树,用于编码大块的信息。默克尔树的酷之处在于,它们是一种自下而上的 "建立",并允许你验证某些值是否存在于树中,而无需在树的每个元素上循环。这可能非常有用,我们会看到。
什么是梅克尔树?
Merkle 树是一种哈希树,其中每个叶子节点都标有数据块的加密哈希值,而每个非叶子节点都标有其子节点标签的加密哈希值。大多数哈希树的实现是二进制的(每个节点有两个子节点),但它们也可以有更多的子节点。
一个典型的 Merkle 树看起来是这样的。
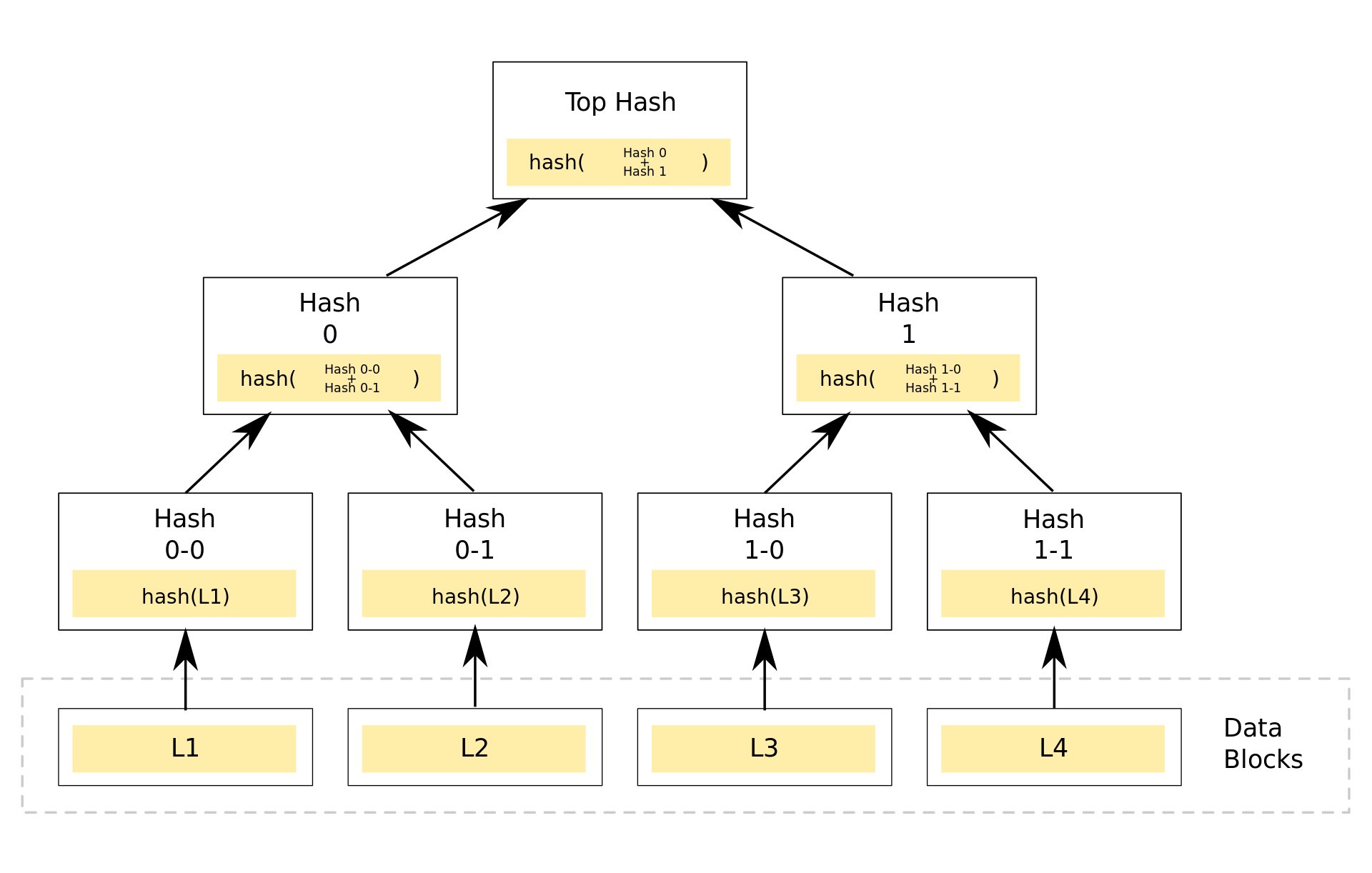
让我解释一下这是怎么回事。树的所有叶子节点,即没有任何进一步子节点的节点,包括你想编码的数据的哈希值。注意,你想在树上编码的值总是只是叶子节点的一部分。因为它是一棵二叉树,每个非叶子节点有两个子节点。当你从叶子节点向上移动时,父节点会有叶子节点的组合哈希值,以此类推。
当你继续这样做时,最终你会在单一的顶级节点上结束,被称为 Merkle 树根,这将会起到非常重要的作用。
简单的例子
假设我们有 4 个交易。所有这些交易都是在同一个区块中执行的,其中包括 "交易 A"、B、C 和 D。这些交易中的每一个都将得到哈希值。让我们把这些哈希值分别称为 "哈希 A"、B、C 和 D。
以下将是这些交易的 Merkle 树的结果。
使用 Merkle Root 验证有效性
当这些交易被卷进一个区块时,区块头将包含 Merkle Root,哈希 ABCD。所有矿工都有一份迄今为止所有交易的副本,因此也有所有交易的哈希值。任何矿工都可以按需重建 Merkle 树,这意味着每个矿工都可以为同一组交易独立得出相同的 Merkle 根。
这使得任何矿工都可以验证一个欺诈性交易。假设有人试图引入一个虚假交易,而不是交易 D,我们称之为交易 E。交易 E 的哈希值是 Hash E。C 和 E 的哈希值是 Hash CE,它与 Hash CD 不同。当哈希 AB 和 CE 被哈希在一起时,你得到哈希 ABCE。由于哈希 ABCE 与哈希 ABCD 不同,我们可以得出结论,交易 E 是欺诈性的。
矿工可以在自己的区块中重新计算 Merkle Root,并试图将该版本发布到区块链上,但由于其他每个矿工都有不同的 Merkle Root,欺诈性的矿工很容易被拒绝。
哈希函数
我们之前在谈论 IPFS 的时候已经介绍了哈希函数,但只是回顾一下:为了将交易 A 哈希成哈希 A,使用了一个单向的加密哈希函数。一旦散列,哈希 A 不能变成交易 A;散列是不可逆的。
每个区块链使用不同的哈希函数,但它们都有相同的共同属性。
确定性
相同的输入在传递到散列函数时总是有相同的输出。
计算效率高
计算一个输入值的哈希值是非常快的。
不能被反转的工程
给出一个哈希值,几乎不可能确定输入值,即哈希函数是单向的函数。例如:给定 y,很难找到一个 x,使 h(x)=y
抗碰撞性
两个不同的输入不会产生相同的输出。
区块链中默克尔树的好处
Merkle Trees 允许快速验证数据的完整性。
与整个交易集相比,所占用的磁盘空间非常小。出于这个原因,Merkle 根被包含在区块头中。
如果你有两组相同的事务,用 Merkle 树来验证它们是否相同,要比一次一次地单独验证事务来得快。人们可以通过了解 Merkle Root 来验证一个区块没有被修改。
区块链之外的用例
Merkle Trees 不只是用于区块链应用。一些使用 Merkle Trees 的流行应用是。
- IPFS
- Git
- 分布式数据库,如 AWS DynamoDB 和 Apache Cassandra 使用 Merkle 树来控制差异性
验证 Merkle 树中的存在
那么,我们如何实际验证一些数据是 Merkle 树的一部分?
你不希望验证器在 Merkle 树的每一个叶子节点上循环,因为它可能相当大,那么我们怎样才能以一种更有效的方式来做这件事?
假设验证器只有 Merkle Root r,也就是树的顶层父节点。作为验证者,你想向验证者证明 Merkle 树中存在某个值 K。
为了做到这一点,你可以生成一个 Merkle 证明。让我们试着用一个 Merkle 树的例子来理解什么是 Merkle 证明。
主要的想法如下:如果你能给验证者 K 的值,以及所有从树上被散列起来的相关节点,以建立 r 散列,验证者可以将计算出的根值与他们已经拥有的 r 进行比较。如果它们是相同的哈希值,这一定意味着 K 实际上存在于 Merkle 树中,因为你不可能用不同的输入数据产生相同的 Merkle 根哈希值。
在上图中,让我们想一想,必须向验证者提供哪些信息,才能向验证者肯定地证明 K 是 Merkle 树的一部分。
- K 本身的值(所以验证者可以自行计算 H(K))。
- H(L),所以验证者可以计算 H(KL)
- H(IJ),所以验证者可以计算 H(IJKL)
- H(MNOP),所以验证者可以计算 H(IJKLMNOP)
- H(ABCDEFGH)所以验证者可以计算 H(ABCDEFGHIJKLMNOP)
同样,重要的是要记住,只有一个给定的节点组合可以产生这个唯��一的根 r,因为 Merkle 树是一个抗碰撞的哈希函数,这意味着它是一个哈希函数,给定两个输入几乎不可能产生相同的输出。
对于我们给定的例子,我们只需要提供以下节点就能够证明 H[K]在我们的节点中实际存在。
在这一点上,如果 H(ABCDEFGHIJKLMNOP)的计算值与验证者先前已知的值 r 相匹配,那么 K 在 Merkle 树中的存在一定是真的,否则哈希值就不一样了。
这比在整个 Merkle 树上进行循环要有效得多,因为对于一个有 n 个元素的树,你只需要提供大约 log(n)个元素作为证明的一部分(树的每个 "层次 "都有一个)。这意味着如果你有大量的数据,Merkle 树比存储数组或映射更有效率。
当 ENS 推出他们的代币合约时,他们向超过 10 万个钱包地址空投了$ENS 代币。他们能够在天然气费用极高的时候部署他们的合约,价格比他们将钱包地址存储在数组中(即使存储几百个地址也很容易超过区块的天然气限制)要低得多 - https://etherscan.io/tx/0xdfc76788b13ab1c033c7cd55fdb7a431b2bc8abe6b19ac9f7d22f4105bb43bff
智能合约中的用例
由于验证器不需要存储整个 Merkle 树来验证某些东西是否是它的一部分,Merkle 树实际上在某些事情上很方便。
在大二时,我们创建了一个白名单 dApp,将用户地址存储在一个映射中。虽然这种方法可行,但在智能合约存储中存储数据是迄今为止最昂贵的事情,你可以在气体方面做。那�么,如果你不得不存储 1000 个地址呢?10,000 个,或者 100,000 个呢?🤯
在这一点上,直接利用智能合约存储就是不可行的,仅仅为了白名单的人就可以轻松地花费数百万美元。另一方面,你可以建立一个 Merkle Tree,并只在合约中存储 Merkle Root 值--一个仅有的字节 32 值。在这种情况下,合约现在是验证者,而那些希望使用他们的白名单位置来铸造 NFT 的用户,比方说,成为证明者,证明他们确实是白名单的一部分。让我们看看这将如何工作。
构建
前提条件
如果你不知道 Mocha 和 Chai 的基础知识,请学习它们,以了解它们是什么,请遵循本教程。
注意 所有这些命令都应该能顺利工作。 如果你在 windows 上遇到错误,比如无法读取 null 的属性(读取'pickAlgorithm'),请尝试使用 npm cache clear --force 清除 NPM 的缓存。
让我们看看这一切对我们的白名单例子是如何实际操作的。
- 要建立一个 Hardhat 项目,打开终端并执行这些命令
npm init --yes
npm install --save-dev hardhat
- 如果你使用的是 Windows 机器,请多做一步,把这些库也安装上 :)
npm install --save-dev @nomicfoundation/hardhat-toolbox @nomiclabs/hardhat-waffle ethereum-waffle chai @nomiclabs/hardhat-ethers ethers
在你安装 Hardhat 的同一目录下运行。
npx hardhat
现在你的 hardhat 文件夹已经设置好了。
我们还需要安装一些额外的依赖。
npm install @openzeppelin/contracts keccak256 merkletreejs
现在开始,在你的 contracts 文件夹中创建一个名为 Whitelist.sol 的文件,并在其中添加以下几行代码
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.4;
import "@openzeppelin/contracts/utils/cryptography/MerkleProof.sol";
contract Whitelist {
bytes32 public merkleRoot;
constructor(bytes32 _merkleRoot) {
merkleRoot = _merkleRoot;
}
function checkInWhitelist(bytes32[] calldata proof, uint64 maxAllowanceToMint) view public returns (bool) {
bytes32 leaf = keccak256(abi.encode(msg.sender, maxAllowanceToMint));
bool verified = MerkleProof.verify(proof, merkleRoot, leaf);
return verified;
}
}
这里到底发生了什么?因此,正如我们提到的,我们没有在合约中存储每个用户的地址,相反,我们只存储 merkle 树的根,在构造函数中被初始化。
我们还有另一个函数 checkInWhitelist,它接收一个证明和 maxAllowanceToMint。maxAllowanceToMint 是一个变量,用于跟踪一个给定地址可以铸造的 NFT 的数量。
对于这个用例,我们在 Merkle 树中实际存储的值是存储用户的地址以及他们被允许铸造的 NFT 数量。你可以在 Merkle 树中存储任何你想要的数据,但这对我们的例子是有效的。这个地址所在的叶子节点的哈希值可以通过首先将发送者的地址和 maxAllowanceToMint 编码成一个字节字符串来计算,然后进一步传递给 keccak256 哈希函数,它需要这个哈希字符串来生成哈希值。
现在我们使用 OpenZeppelin 的 MerkleProof 库来验证用户发送的证明确实有效。注意 Openzeppelin 如何在高层次上进行验证,与我们在教程前面谈到的 Merkle 证明的验证相似。
接下来,让我们写一个测试,它可以帮助确定我们合约中的代码是否真的有效。
在你的测试文件夹中创建一个新的文件 merkle-root.js,并在其中添加以下几行代码
const { expect } = require("chai");
const { ethers } = require("hardhat");
const keccak256 = require("keccak256");
const { MerkleTree } = require("merkletreejs");
function encodeLeaf(address, spots) {
// Same as `abi.encodePacked` in Solidity
return ethers.utils.defaultAbiCoder.encode(
["address", "uint64"],
[address, spots]
);
}
describe("Check if merkle root is working", function () {
it("Should be able to verify if a given address is in whitelist or not", async function () {
// Get a bunch of test addresses
const [owner, addr1, addr2, addr3, addr4, addr5] =
await ethers.getSigners();
// Create an array of elements you wish to encode in the Merkle Tree
const list = [
encodeLeaf(owner.address, 2),
encodeLeaf(addr1.address, 2),
encodeLeaf(addr2.address, 2),
encodeLeaf(addr3.address, 2),
encodeLeaf(addr4.address, 2),
encodeLeaf(addr5.address, 2),
];
// Create the Merkle Tree using the hashing algorithm `keccak256`
// Make sure to sort the tree so that it can be produced deterministically regardless
// of the order of the input list
const merkleTree = new MerkleTree(list, keccak256, {
hashLeaves: true,
sortPairs: true,
});
// Compute the Merkle Root
const root = merkleTree.getHexRoot();
// Deploy the Whitelist contract
const whitelist = await ethers.getContractFactory("Whitelist");
const Whitelist = await whitelist.deploy(root);
await Whitelist.deployed();
// Compute the Merkle Proof of the owner address (0'th item in list)
// off-chain. The leaf node is the hash of that value.
const leaf = keccak256(list[0]);
const proof = merkleTree.getHexProof(leaf);
// Provide the Merkle Proof to the contract, and ensure that it can verify
// that this leaf node was indeed part of the Merkle Tree
let verified = await Whitelist.checkInWhitelist(proof, 2);
expect(verified).to.equal(true);
// Provide an invalid Merkle Proof to the contract, and ensure that
// it can verify that this leaf node was NOT part of the Merkle Tree
verified = await Whitelist.checkInWhitelist([], 2);
expect(verified).to.equal(false);
});
});
在这里,我们首先使用 hardhat 的扩展 ethers 包获得一些签名者进行测试。
然后我们创建一个节点列表,使用 ethers.utils.defaultAbiCoder.encode 将其全部转换为字节字符串。
使用 merkletreejs 中的 MerkleTree 类,我们输入我们的列表,指定我们的散列函数(将是 keccak256),并将节点的排序设置为 true。
在我们创建 Merkle Tree 之后,我们通过调用 getHexRoot 函数来获得其根。我们用这个根来部署我们的白名单合约。
在我们的契约被验证后,我们可以通过提供证明来调用我们的 checkInWhitelist。所以现在在这里我们将检查(owner.address, 2)在我们的数据集中是否存在。为了生成证明,我们对(owner.address, 2)的编码值进行散列,并使用 merkletreejs 库的 getHexProof 函数生成一个证明。
然后,这个证明作为一个参数被送入 checkInWhitelist,进一步返回一个真值,表示(owner.address, 2)存在。
要运行该测试,请从目录根部执行以下命令。
npx hardhat test
如果你的所有测试都通过了,你就成功地学会了什么是默克尔树,以及如何将其用于白名单。
贡献者
本模块是与 Hypotenuse 实验室合作完成的。